Termodynamika - 7.03 zadanie
zadanie
Gazy rzeczywiste w pewnym zakresie parametrów można traktować jak gaz doskonały (idealny). Temperatura gazu doskonałego T jest proporcjonalna do średniej energii kinetycznej ruchu postępowego jego cząsteczek. Dla gazu doskonałego spełnione jest równanie Clapeyrona.
a) Uzupełnij zdania, podkreślając poprawne stwierdzenia, tak aby opisywały gaz według modelu gazu doskonałego.
1. Rozmiary cząsteczek i zajmowaną przez nie objętość uwzględniamy / pomijamy.
2. Cząsteczki gazu oddziałują ze sobą tylko podczas zderzeń / także na odległość.
3. Zderzenia cząsteczek ze sobą i ściankami naczynia są sprężyste / niesprężyste.
b) Powietrze jest mieszaniną gazów, m.in. tlenu
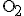 (masa molowa 32 g/mol), azotu
(masa molowa 32 g/mol), azotu 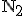 (masa molowa 28 g/mol) i argonu Ar (masa molowa 40 g/mol). Określ zależność między średnimi prędkościami tych cząsteczek, wpisując w lukach znaki wybrane spośród =, > i <.
(masa molowa 28 g/mol) i argonu Ar (masa molowa 40 g/mol). Określ zależność między średnimi prędkościami tych cząsteczek, wpisując w lukach znaki wybrane spośród =, > i <.Przez średnią prędkość rozumiemy tu średnią wartość wektora prędkości.
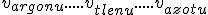
c)
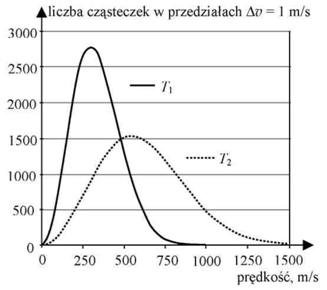
Podane wyżej wykresy przedstawiają tzw. rozkład Maxwella.
Na osi pionowej odłożono liczbę cząsteczek gazu, których wartości prędkości leżą w przedziale od
 do
do 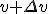 , dla szerokości przedziału
, dla szerokości przedziału 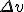 równej 1 m/s. Wykresy wykonano dla jednego miliona cząsteczek gazu o temperaturze
równej 1 m/s. Wykresy wykonano dla jednego miliona cząsteczek gazu o temperaturze 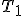 i o temperaturze
i o temperaturze 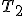 . Podaj, która z temperatur
. Podaj, która z temperatur 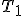 i
i 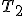 jest wyższa. Uzasadnij odpowiedź.
jest wyższa. Uzasadnij odpowiedź.d) Jeden mol gazu doskonałego o temperaturze początkowej
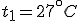 i ciśnieniu początkowym
i ciśnieniu początkowym 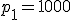 hPa ogrzano izobarycznie o
hPa ogrzano izobarycznie o 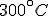 , a następnie izochorycznie o kolejne
, a następnie izochorycznie o kolejne 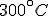 . Oblicz końcowe ciśnienie gazu
. Oblicz końcowe ciśnienie gazu 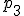 .
.Informacja do zadań e) i f)
Dla gazu rzeczywistego zamiast równania Clapeyrona stosuje się równanie van der Waalsa, które dla n moli gazu ma postać
 \( V-bn\) = nRT)
Współczynniki a i b uwzględniają odstępstwa od modelu gazu doskonałego dla gazów rzeczywistych i zależą od rodzaju gazu, np. dla dwutlenku węgla wynoszą odpowiednio
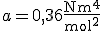 i
i 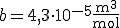
e) Korzystając z równania van der Waalsa, oblicz ciśnienie 1 mola dwutlenku węgla o temperaturze 300 K, zamkniętego w zbiorniku o objętości
 .
.f) Przyjmijmy, że gaz stosuje się do modelu gazu doskonałego, gdy ciśnienie gazu obliczone z równania Clapeyrona nie różni się od ciśnienia rzeczywistego o więcej niż 10%. Dla 1 mola pewnego gazu rzeczywistego o temperaturze 300 K zamkniętego w zbiorniku o objętości
 ciśnienie jest równe 1,15 MPa. Wykonaj niezbędne obliczenia i ustal, czy ten gaz może być traktowany jak gaz doskonały.
ciśnienie jest równe 1,15 MPa. Wykonaj niezbędne obliczenia i ustal, czy ten gaz może być traktowany jak gaz doskonały.Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.