Moment bezwładnościkurs
Moment bezwładności bryły względem danej osi.
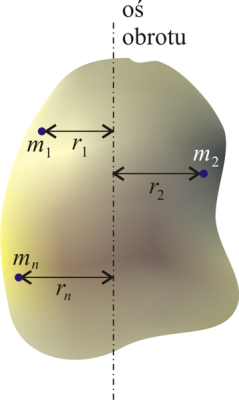
Jeżeli bryła dzieli się na punkty o masach
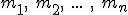oddalonych od osi obrotu o 
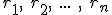, to momentem bezwładności bryły względem tej osi obrotu nazywamy wyrażenie: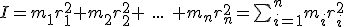
Dla brył ciągłych definicja jest bardziej skomplikowana, wymaga znajomości rachunku całkowego.
Z definicji wynika, że z dwóch brył o równych masach, ta ma większy moment bezwładności, której punkty są bardziej oddalone od osi obrotu. Moment bezwładności mówi nam nie tylko masie bryły lecz i o tym, jak masa jest rozłożona względem osi obrotu. Przesunięcie lub zmiana kierunku osi obrotu względem bryły sztywnej powoduje zmianę momentu bezwładności, zatem nie jest to stała cecha ciała.
Dalsza część kursu dostępna
dla użytkowników 
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.