Równania wymiernekurs
}{V(x)}=0)
,)
i )
wielomiany.Rozwiązywanie takich równań sprowadza się włściwie do rozwiązywania równań wielomianowych.
Rozwiązanie równania
jest równoważne:=0)
i \neq 0)
.Ułamek jest równy zero, gdy jego licznik jest równy zero, natomiast mianownik musi być różny od zera, bo w przeciwnym razie ułamek nie będzie miał sensu liczbowego.
Przykład 1
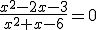
To równanie jest równoważne:
1)
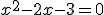i 2)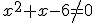 
1)
^2-4\cdot1\cdot(-3)=16 \\ \sqrt{\Delta}=4 \\ x_1=-1, \ \ \ x_2=3)
2)
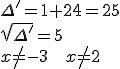
Ostatecznie rozwiązaniami równania są:
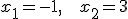
Przykład 2
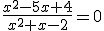
To równanie jest równoważne:
1)
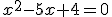i 2)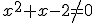 
1)
^2-4\cdot1\cdot4=9 \\ \sqrt{\Delta}=3 \\ x_1=1, \ \ \ x_2=4)
2)
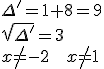
Ostatecznie rozwiązaniami równania jest:
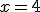
bo
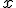nie może być równe 
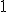; nie należy ono do dziedziny równania. Dziedzina to zbiór tych liczb, dla których wyrażenie algebraiczne po lewej stronie równania ma sens.Dalsza część kursu dostępna
dla użytkowników 
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.