Elementy rachunku prawdopodobieństwakurs
Jest to zdarzenie, którego wyniku nie możemy przewidzieć. Znamy tylko zestaw możliwych wyników takiego zdarzenia. Klasycznym przykładem jest rzut kostką. Nie sposób przewidzieć ile oczek wypadnie, wiemy tylko, że musi to być jedna z liczb 1, 2, 3, 4, 5, 6.
Zdarzenie elementarne.
Pewne zdarzenia można zrealizować na wiele sposobów. Na przykład zdarzenie: na kostce wypadnie liczba nieparzysta może być zrealizowane na trzy sposoby: może wypaść 1, 3 lub 5. Inne zdarzenia mogą się realizować tylko w jeden sposób. Wyrzucić "szóstkę" na kostce można tylko w jeden sposób, właśnie wyrzucając "szóstkę". Zdarzenia, które można zrealizować na jeden sposób nazywają się zdarzeniami elementarnymi. To oczywiście nie jest żadna definicja, tylko tak, żeby wiedzieć o co chodzi. Definicji zdarzenia elementarnego nie ma, bo jest to pojęcie pierwotne rachunku prawdopodobieństwa. Inne przykłady takich zdarzeń:
- wyrzucenie orła w jednokrotnym rzucie monetą
- wyciągnięcie asa pik, gdy ciągniemy jedną kartę z talii
- wyrzucenie dwóch piątek w dwukrotnym rzucie kostką
- i wiele innych
Zdarzenia elementarne oznacza się zwykle grecką literą
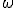 .
.Zbiór zdarzeń elementarnych. To jest oczywiście zbiór wszystkich zdarzeń elementarnych. Nic tu właściwie nie powiedziałem powtórzyłem tylko sformułowanie z tytułu. Zbiór ten oznaczamy
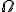 .
.Nie zawsze łatwo wskazać wszystkie zdarzenia elementarne. Można jednak powiedzieć jakie warunki zdarzenia muszą spełniać, by były elementarne i tworzyły cały zbiór zdarzeń elementarnych.
1. Każde zdarzenie elementarne musi być rozłączne z każdym innym. Zatem, jeżeli wynikiem doświadczenia losowego jest jakieś zdarzenie elementarne, to nie może trafić się w tym samym zdarzeniu żadne inne zdarzenie elementarne.
2. Lista zdarzeń elementarnych musi być kompletna, to znaczy, że nie jest możliwy wynik jakiegokolwiek zdarzenia spoza tej listy.
Zdarzeniem będziemy nazywać dowolny podzbiór zbioru zdarzeń elementarnych.
Przykład.
W pojedynczym rzucie kostką może wypaść jedna z sześciu liczb. I tylko jedna. Te liczby to 1, 2, 3, 4, 5, 6. To są wszystkie wyniki, którymi może zakończyć się rzut kostką. To są zdarzenia elementarne. A jakie są przykłady zdarzeń niekoniecznie elementarnych? Takim zdarzeniem będzie wyrzucenie parzystej liczby oczek. Jakie zdarzenia elementarne składają się na to zdarzenie? Są to 2, 4, 6. Mamy więc podzbiór zbioru zdarzeń elementarnych {2, 4, 6}.
W klasycznej definicji prawdopodobieństwa, której autorem jest Pierre Simon de Laplace, zakłada się, że wszystkie zdarzenie elementarne są jednakowo prawdopodobne. Jest taka sama szansa wystąpienia każdego ze zdarzeń elementarnych.
Jeżeli wszystkie zdarzenia elementarne są równoprawdopodobne, to prawdopodobieństwo każdego zdarzenia
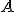 jest ilorazem liczby zdarzeń elementarnych sprzyjających temu zdarzeniu przez liczbę wszystkich zdarzeń elementarnych.
jest ilorazem liczby zdarzeń elementarnych sprzyjających temu zdarzeniu przez liczbę wszystkich zdarzeń elementarnych.Co to znaczy zdarzenie elementarne sprzyjające danemu zdarzeniu? Pamiętamy, że zdarzenie jest podzbiorem zbioru zdarzeń elementarnych. Wszystkie zdarzenia elementarne, które zawierają się w tym podzbiorze, to zdarzenia sprzyjające.
Poszukiwanie prawdopodobieństwa jakiegoś zdarzenia według schematu klasycznego odbywa się według następującego planu:
1) Określamy co jest zdarzeniem elementarnym.
2) Rozstrzygamy czy zdarzenia elementarne są jednakowo prawdopodobne. Jeśli nie, szukamy inaczej określonych zdarzeń elementarnych.
3) Znajdujemy liczbę wszystkich zdarzeń elementarnych
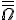 .
.4) Znajdujemy te zdarzenia elementarne, które sprzyjają zdarzeniu
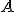 , którego prawdopodobieństwo mamy obliczyć.
, którego prawdopodobieństwo mamy obliczyć.5) Znajdujemy liczbę zdarzeń elementarnych sprzyjających zdarzeniu
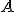 -
- 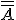 .
.6) Korzystamy z klasycznej definicji prawdopodobieństwa -
=\frac{\bar{\bar{A}}}{\bar{\bar{\Omega}}}) .
.Własności prawdopodobieństwa
Niech
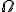 będzie danym skończonym zbiorem zdarzeń elementarnych. Każdemu zdarzeniu
będzie danym skończonym zbiorem zdarzeń elementarnych. Każdemu zdarzeniu 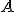 zawartemu w
zawartemu w 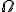 jest przyporządkowana dokładnie jedna liczba zwana prawdopodobieństwem zdarzenia
jest przyporządkowana dokładnie jedna liczba zwana prawdopodobieństwem zdarzenia 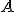 taka, że
taka, że1)
 \leq 1)
2)
=1)
3) dla każdej pary rozłącznych (wykluczających się) zdarzeń
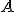 i
i 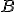 zachodzi
zachodzi =P(A)+P(B)) .
.Dodam jeszcze, że pewne zdarzenia na pewno zajść nie mogą i ich prawdopodobieństwo jest równe zeru. Oznaczmy je
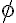 . Wtedy
. Wtedy =0) . Oznaczenie to jest zarazem oznaczeniem zbioru pustego. Zdarzenie niemożliwe nie zawiera żadnego zdarzenia elementarnego, dlatego takie oznaczenie jest usprawiedliwione.
. Oznaczenie to jest zarazem oznaczeniem zbioru pustego. Zdarzenie niemożliwe nie zawiera żadnego zdarzenia elementarnego, dlatego takie oznaczenie jest usprawiedliwione. Jeśli zdarzenie jest tak określone, że zawiera wszystkie zdarzenia elementarne
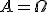 , to zdarzenie takie w danym doświadczeniu na pewno zajdzie i jego prawdopodobieństwo wynosi 1. Zdarzenie takie nazwiemy pewnym. Inaczej możemy powiedzieć, że jeśli już robimy jakieś doświadczenie losowe (na przykład rzucamy kostką), to prawdopodobieństwo, że otrzymamy jakikolwiek wynik jest równe 1.
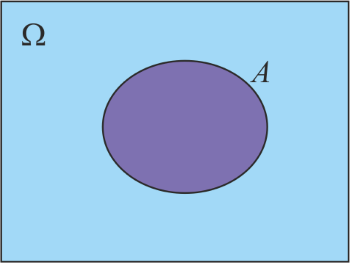
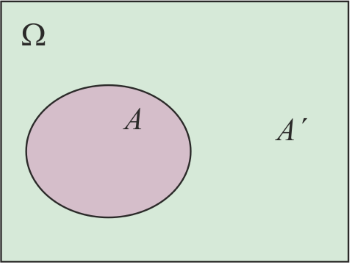
, to zdarzenie takie w danym doświadczeniu na pewno zajdzie i jego prawdopodobieństwo wynosi 1. Zdarzenie takie nazwiemy pewnym. Inaczej możemy powiedzieć, że jeśli już robimy jakieś doświadczenie losowe (na przykład rzucamy kostką), to prawdopodobieństwo, że otrzymamy jakikolwiek wynik jest równe 1.Nie od rzeczy będzie powiedzieć coś o graficznym przedstawieniu prawdopodobieństwie. Nie będzie to ścisłe, ale za to obrazowe i pewne twierdzenia dotyczące prawdopodobieństwa łatwo będzie za pomocą tej metody przedstawić. Przedstawmy mianowicie zbiór zdarzeń elementarnych w postaci prostokąta.

Zdarzenie
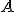 , które jak wiemy, jest podzbiorem zbioru zdarzeń elementarnych można wtedy przedstawić w postaci kółka zawartego w tym prostokącie. Za prawdopodobieństwo zdarzenia
, które jak wiemy, jest podzbiorem zbioru zdarzeń elementarnych można wtedy przedstawić w postaci kółka zawartego w tym prostokącie. Za prawdopodobieństwo zdarzenia 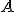 można w takim modelu uważać stosunek pól: kółka reprezentującego zdarzenie
można w takim modelu uważać stosunek pól: kółka reprezentującego zdarzenie 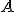 i prostokąta reprezentującego zbiór zdarzeń elementarnych
i prostokąta reprezentującego zbiór zdarzeń elementarnych 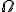 .
. 
A teraz pozostałe własności prawdopodobieństwa. Tam, gdzie to będzie pożądane, zilustruję własność rysunkiem.
1)
=0) (to już było)
(to już było)2) Jeżeli
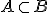 , to
, to \leq P(B)) .
. 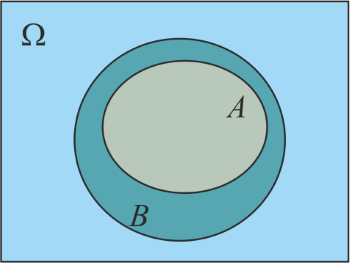
Jasne jest, że jeśli podzielimy pole kółka
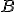 przez pole prostokąta, to otrzymamy coś większego (lub równego, bo bycie podzbiorem obejmuje również równość zbiorów jako szczególny przypadek), niż gdybyśmy dzielili pole kółka
przez pole prostokąta, to otrzymamy coś większego (lub równego, bo bycie podzbiorem obejmuje również równość zbiorów jako szczególny przypadek), niż gdybyśmy dzielili pole kółka 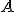 przez pole tegoż prostokąta.
przez pole tegoż prostokąta. 3) Dla każdego
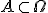 ,
, \leq 1) . To też było.
. To też było.4)
=1-P(A)) .
.Co to jest
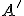 ? Jest to zdarzenie przeciwne do
? Jest to zdarzenie przeciwne do 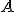 . Mówiąc językiem teorii zbiorów jest to dopełnienie zbioru
. Mówiąc językiem teorii zbiorów jest to dopełnienie zbioru 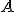 do
do 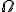 . Mówiąc prościej: zdarzeniem przeciwnym do danego jest podzbiór tych wszystkich zdarzeń elementarnych które nie należą do zdarzenia
. Mówiąc prościej: zdarzeniem przeciwnym do danego jest podzbiór tych wszystkich zdarzeń elementarnych które nie należą do zdarzenia 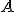 . Myślę, że dla większej jasności nieodzowny będzie przykład.
. Myślę, że dla większej jasności nieodzowny będzie przykład.Przykład.
Zdarzeniem będzie pojedynczy rzut kostką. Zbiór zdarzeń elementarnych to
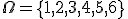 . Niech zdarzenie
. Niech zdarzenie 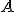 polega na tym, że wyrzucono liczbę oczek podzielną przez
polega na tym, że wyrzucono liczbę oczek podzielną przez 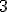 . Zdarzeniu temu sprzyjają "trójka" i "szóstka", zatem
. Zdarzeniu temu sprzyjają "trójka" i "szóstka", zatem 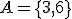 . Jakie jest zdarzenie przeciwne do
. Jakie jest zdarzenie przeciwne do 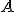 ? Zdarzenie to polega na tym, że wyrzucono liczbę oczek, która nie jest podzielna przez
? Zdarzenie to polega na tym, że wyrzucono liczbę oczek, która nie jest podzielna przez 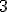 . Temu zdarzeniu sprzyjają wszystkie pozostałe zdarzenia elementarne.
. Temu zdarzeniu sprzyjają wszystkie pozostałe zdarzenia elementarne. 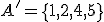 .
.Zilustruję to jeszcze.
Zdarzenie
 to niebieskie kółko, a
to niebieskie kółko, a  to cała reszta zbioru
to cała reszta zbioru  .
.Wzór ten jest często wykorzystywany w zadaniach.
5)
=P(A)+P(B)-P(A\cap B)) .
.Ten wzór też jest często wykorzystywany.
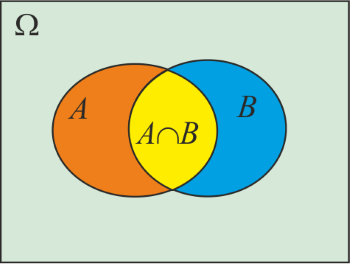
Czym są zdarzenia
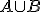 i
i  ? Są to: suma zdarzeń i iloczyn zdarzeń, czyli ich część wspólna. Zobaczmy to na przykładzie, jak zwykle z rzutem kostką.
? Są to: suma zdarzeń i iloczyn zdarzeń, czyli ich część wspólna. Zobaczmy to na przykładzie, jak zwykle z rzutem kostką.Niech
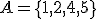 ,
, 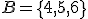 . Wtedy
. Wtedy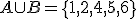 i
i 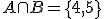
Dalsza część kursu dostępna
dla użytkowników  premium
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.