SOFIZMAT

Reguła mnożenia

Na poziomie podstawowym najważniejsza w kombinatoryce jest zasada mnożenia. Na czym ona polega?
Przykład 1
Idziemy do restauracji i chcemy zjeść obiad z dwóch dań: zupę i drugie danie. Okazuje się, że mamy do wyboru trzy zupy (rosół, zupa grzybowa i pomidorowa) i cztery drugie dania (schabowy, placek po węgiersku, spaghetti i filet z kurczaka). Ile różnych posiłków możemy zamówić? Na przykład możemy wybrać rosół, a do tego dobrać drugie danie na cztery sposoby, wybrać grzybową itd. Wszystkie wybory możemy zobaczyć na rysunku poniżej.

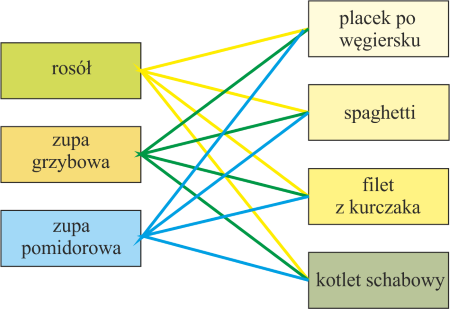
Łatwo policzyć (licząc kolorowe linie), że możemy utworzyć 12 par zupa - drugie danie.
Do każdej z trzech zup możemy dobrać każde z czterech drugich dań. Zatem wszystkich możliwości jest .
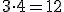Przykład 2
Rzucamy monetą i kostką do gry. Ile jest wyników takiego rzutu?

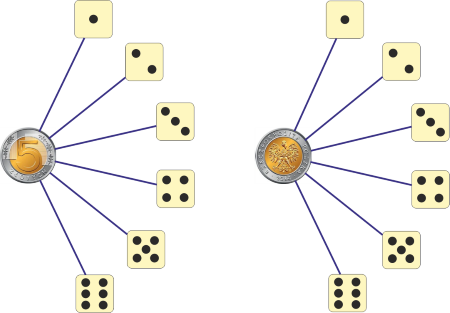
Mamy dwie możliwości wyniku rzutu monetą i sześć rzutu kostką. Widzimy (rysunek), że wszystkich możliwości jest 12. Rzeczywiście tyle otrzymamy mnożąc liczbę możliwości rzutu monetą przez liczbę możliwości rzutu kostką. .
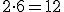Reguła mnożenia dla czynności dwuetapowej
Jeżeli pewną czynność wykonuje się w dwóch etapach, przy czym etap pierwszy można wykonać na 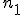sposobów, a drugi na 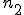sposobów, to liczba sposobów 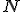jakimi można wykonać tę czynność wyraża się wzorem: .
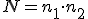Tę właśnie zasadę mnożenia wykorzystywaliśmy w powyższych przykładach. Zasadę tę można uogólnić.
Reguła mnożenia dla k-etapowej czynności
Jeśli pewną czynność wykonuje się w k-etapach, przy czym: etap 1 można wykonać na 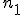sposobów, etap 2 na 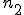sposobów, , wreszcie 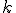-ty etap na 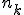sposobów, to liczba 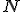sposobów, jakimi można wykonać tę czynność wyraża się wzorem: .
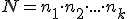Przykład 3
Ile jest możliwych wyników doświadczenia polegającego na trzykrotnym rzucie kostką?
Wykorzystajmy regułę mnożenia. Mamy tu czynność, w której wyróżniamy trzy etapy - pierwszy, drugi i trzeci rzut. Każdy z rzutów może się skończyć na 6 sposobów. Wobec tego liczba możliwości jakie mamy w trzykrotnym rzucie wynosi:
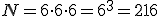
Jeśli w pierwszym rzucie wyrzucimy szóstkę, w drugim i trzecim też ta szóstka może się pojawić. Wyniki mogą powtarzać się w różnych etapach. Taką sytuację, takie pojęcie kombinatoryczne nazywamy wariacją z powtórzeniami.
Przykład 4
W trzydziestoosobowej klasie odbywają się wybory samorządu. Do obsadzenia są stanowiska: przewodniczącego, jego zastępcy i skarbnika. Na ile sposobów mogą skończyć się takie wybory, albo inaczej, ile różnych trzyosobowych samorządów można utworzyć w tej klasie? Za różne samorządy będziemy uważać takie, które mają różne składy osobowe (różnią się przynajmniej jedną osobą) lub takie, które mają ten sam skład osobowy ale stanowiska różnie obsadzone.
Tym razem wyniki poszczególnych etapów nie mogą się powtórzyć, bo nie można wybrać tej samej osoby na stanowisko przewodniczącego i zastępcy lub skarbnika. Zatem przewodniczącego można wybrać na 30 sposobów, ale zastępcę już na 29 sposobów (jednej osoby - tej, która została przewodniczącym - nie da się drugi raz wybrać), a skarbnika na 28 sposobów. Korzystamy z reguły mnożenia, by uzyskać odpowiedź na nasze pytanie.
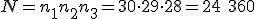. Tyle samorządów można utworzyć w 30-osobowej klasie.
W tym przypadku wyniki w kolejnych etapach nie mogą się powtarzać. Są to wariacje bez powtórzeń
Przykład 5
Ustawiamy 6 książek na półce. Na ile sposobów można to zrobić?

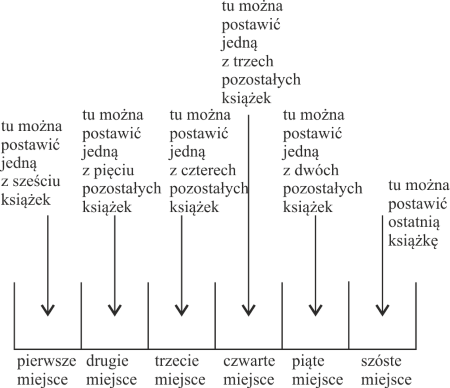
Nie można tej samej książki postawić jednocześnie na dwóch miejscach. Jeśli na pierwszym miejscu postawimy, wybrawszy z sześciu, jedną, to nie postawimy jej już na żadnym innym miejscu. Zatem pierwsze miejsce na półce można wypełnić na sześć sposobów, drugie na pięć, trzecie na cztery itd. Korzystamy z reguły mnożenia i otrzymujemy:

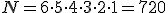
Iloczyn liczb naturalnych od 1 do , czyli nazywamy silnią i oznaczamy