Równania prostejkurs
)
. W tymże punkcie przecinają się dwie prostopadłe do siebie osie liczbowe. Punkt, którego współrzędne chcemy znać rzutujemy prostopadle na obie osie i odczytujemy liczby na osiach, które tym rzutom odpowiadają, a potem ustawiamy te liczby w parę. pierwszym elementem pary jest liczba odczytana z poziomej osi, drugim - liczba odczytana z drugiej osi. Pierwszą z liczb nazywamy odciętą, drugą - rzędną.
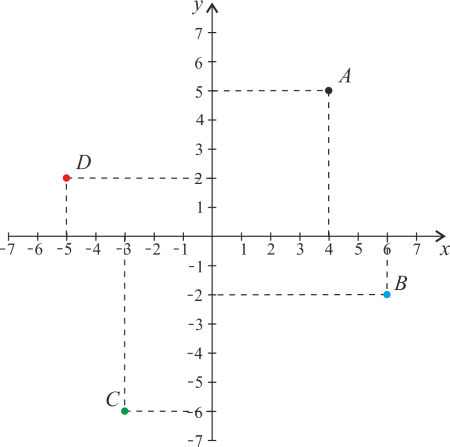
Na powyższym rysunku cztery punkty mają następujące współrzędne:
)
, )
, )
, )
.Tyle o położeniu punktów.
Jak opisywać złożone z punktów a bardziej złożone figury? Jeśli figura jest regularna, to punkty nie są poukładane byle jak, tylko ich współrzędne są jakoś ze sobą związane. Taki związek może mieć postać równania lub nierówności.
Dalsza część kursu dostępna
dla użytkowników 
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.