Własności ciągówkurs
Monotoniczność to własność niektórych ciągów. Ciąg monotoniczny to zbiorcza nazwa czterech przypadków:
a) ciąg rosnący
Ciąg rosnący to taki, którego kolejne wyrazy są coraz większe. Mówiąc inaczej: jeśli weźmiemy dowolny wyraz tego ciągu
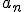 to wyraz następny, czyli
to wyraz następny, czyli 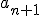 będzie większy od
będzie większy od 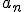 . Zapisując to w nieco bardziej formalny sposób: ciąg jest rosnący wtedy, gdy dla każdego
. Zapisując to w nieco bardziej formalny sposób: ciąg jest rosnący wtedy, gdy dla każdego 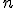 :
: 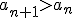 .
. Na rysunku wygląda to na przykład tak
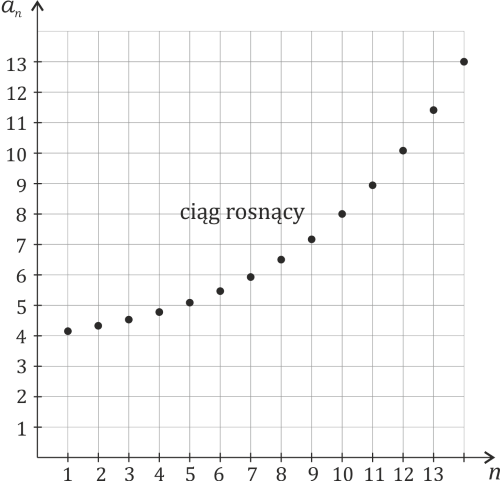
Przykłady ciągów rosnących:
1)
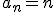 - to chyba najprostszy przykład.
- to chyba najprostszy przykład.2)
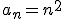
3)
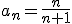
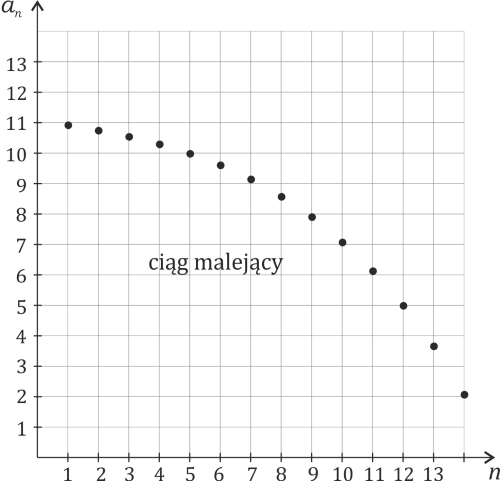
b) ciąg malejący
Ciąg malejący, to taki, którego wyrazy maleją wraz ze wzrostem
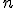 . Inaczej: ciąg jest malejący wtedy, gdy dla każdego
. Inaczej: ciąg jest malejący wtedy, gdy dla każdego 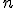
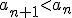
Przykład rysunkowy
c) ciąg niemalejący
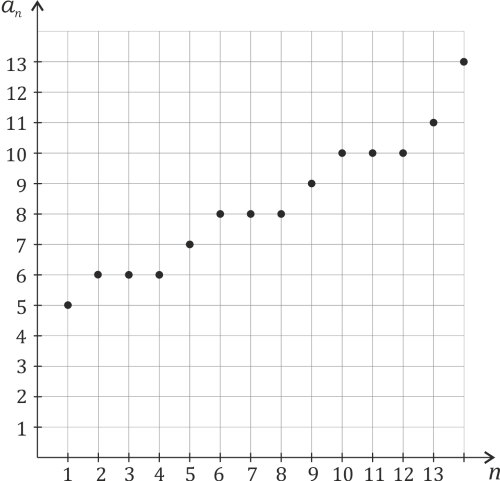
Ciąg niemalejący to taki który, jak sama nazwa wskazuje, nie maleje. Pozostają więc dwie możliwości: albo wyrazy są większe od swych poprzedników, albo im równe. Zatem ciąg niemalejący to taki, że dla każdego
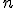 zachodzi
zachodzi 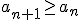 .
.
d) ciąg nierosnący
Wyrazy ciągu nierosnącego nie rosną. Pozostają więc takie same lub maleją. Ciąg nierosnący to ciąg, który dla każdego
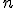 spełnia zależność
spełnia zależność 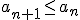 .
.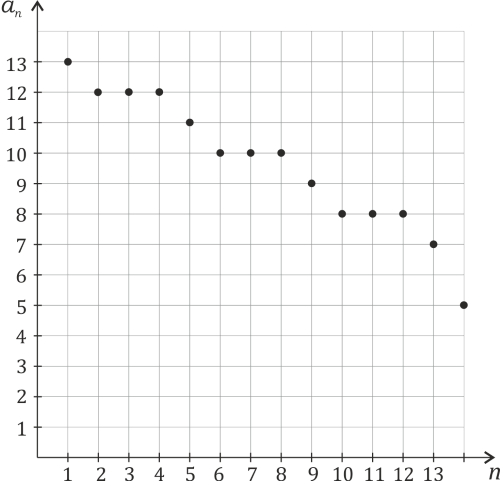
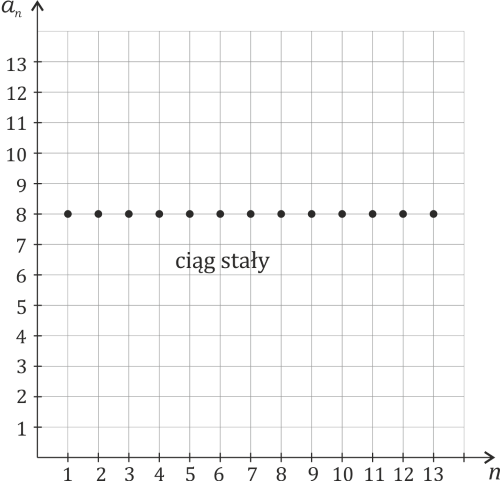
Ciąg, który jednocześnie jest nierosnący i niemalejący, to ciąg stały.
Ciąg nie musi wcale należeć do któregoś z powyższych typów - nie musi być rosnący lub malejący dla wszystkich
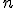 . Może być niemonotoniczny. Na przykład taki, jak na poniższym rysunku.
. Może być niemonotoniczny. Na przykład taki, jak na poniższym rysunku.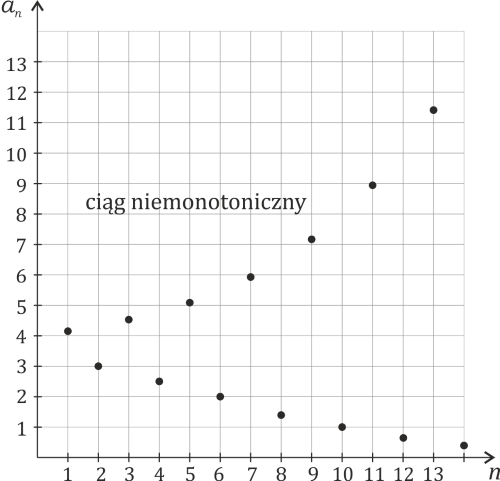
Albo taki
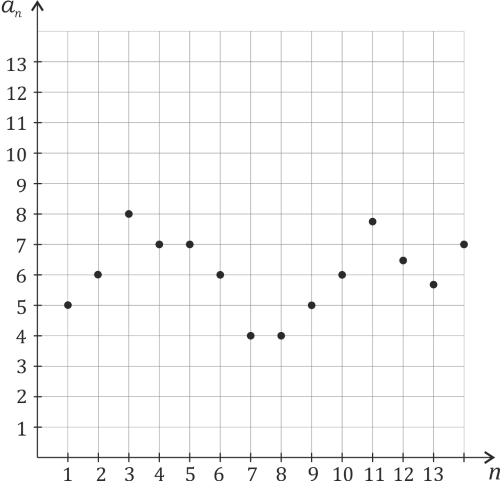
Ciągi ograniczone i nieograniczone
Ciąg może być ograniczony na trzy sposoby: z góry, z dołu i w ogóle. Zacznijmy może od ciągu ograniczonego z góry. To ograniczenie oznacza, że istnieje największy wyraz ciągu, albo inaczej istnieje taka liczba której nie przekracza żaden wyraz ciągu. W nieco bardziej sformalizowany sposób: ciąg jest ograniczony z góry wtedy, gdy istnieje taka liczba
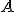 , że dla każdego wyrazu ciągu (dla każdego
, że dla każdego wyrazu ciągu (dla każdego 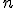 ) zachodzi
) zachodzi 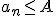 .
.Ciąg jest ograniczony z dołu, jeśli każdy wyraz ciągu jest większy lub równy niż pewna liczba. Inaczej: ciąg jest ograniczony z dołu wtedy, gdy istnieje liczba
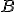 taka, że każdy wyraz ciągu spełnia zależność
taka, że każdy wyraz ciągu spełnia zależność 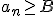 .
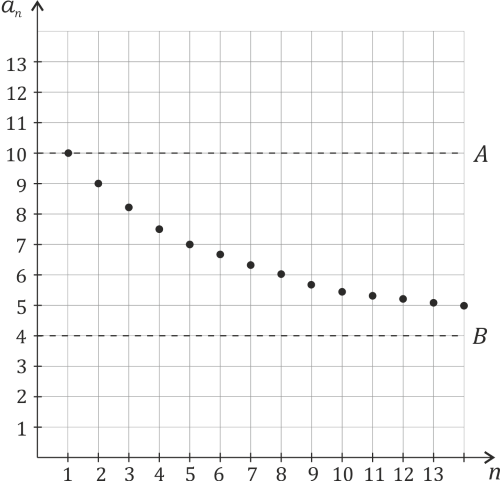
.Ciąg jest ograniczony, gdy jest ograniczony zarówno z góry, jak i z dołu. Istnieją wtedy liczby
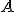 i
i 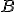 takie, że dla każdego
takie, że dla każdego 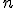 zachodzi
zachodzi 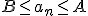 .
.
Ciągi nieograniczone to takie, których wyrazy mogą być dowolnie duże, lub dowolnie małe. Dowolnie duże to takie, że jkąkolwiek liczbę byście podali, to znajdzie się wyraz ciągu większy od niej. Najprostszym przykładem ciągu nieograniczonego z góry jest
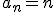
Przykładem ciągu nieograniczonego z dołu jest
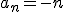
Ciągiem ograniczonym jest
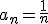 , bo
, bo 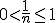 .
.Dalsza część kursu dostępna
dla użytkowników  premium
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.