Ciąg geometrycznykurs
)
.Próby odgadnięcia, jak jest on skonstruowany szybko doprowadziłyby do wniosku, że każdy (prócz pierwszego) wyraz otrzymamy, jeżeli poprzedni pomnożymy przez trzy.
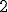
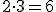
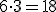
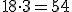
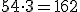
itd.
Mnożenie przez stały czynnik to charakterystyczna cecha ciągu geometrycznego. Oto jego definicja:
Ciąg geometryczny to taki ciąg w którym każdy wyraz oprócz pierwszego powstaje przez pomnożenie poprzedniego przez stałą liczbę
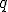zwaną ilorazem ciągu geometrycznego.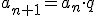 
To jest rekurencyjny wzór dla ciągu geometrycznego.
Nietrudno znaleźć wzór na ogólny wyraz ciągu geometrycznego. Argumenty za takim wzorem są analogiczne jak dla ciągu arytmetycznego.
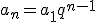
Dla każdych trzech kolejnych wyrazów ciągu geometrycznego obowiązuje analogiczny wzór jak dla ciągu arytmetycznego.
Wiadomo, że
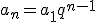. Z tego wzoru wynika, że 
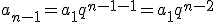, oraz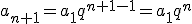 
^2=a_n^2)
.Zatem
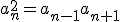
Suma
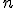początkowych wyrazów ciągu geometrycznegoOznaczmy sumę
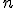początkowych wyrazów ciągu 
.
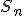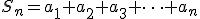
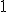 \ S_n=a_1+a_1q+a_1q^2+a_1q^3+\dots +a_1q^{n-1})
Pomnóżmy wyrażenie 1) przez
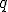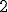. \ qS_n=a_1q+a_1q^2+a_1q^3+\dots +a_1q^{n-1}+a_1q^n)
Odejmijmy stronami 2) i 1).
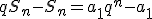
=a_1(q^n-1))
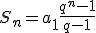
To jest właśnie wzór na sumę
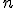początkowych wyrazów ciągu geometrycznego. Ma on jednak pewne ograniczenie. Mianowicie nie działa, gdy 
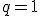, ze względu na zero w mianowniku w takim przypadku. Jeśli 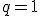, mamy do czynienia z ciągiem stałym )
. W takiej sytuacji suma wynosi po prostu 
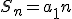
Zatem kompletny wzór na sumę ma postać:
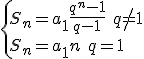
Czy ciąg może być jednocześnie geometryczny i arytmetyczny? Tak. Wtedy, gdy jest to ciąg stały. Wtedy
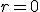i 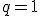.Dalsza część kursu dostępna
dla użytkowników 
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.