Ciąg arytmetycznykurs
)
Co jest w nim charakterystycznego? To, że jeśli do dowolnego wyrazu ciągu dodamy 4, to otrzymamy następny. Jest to charakterystyczne dla ciągu arytmetycznego. Albo inaczej: różnica między dowolnym wyrazem a jego poprzednikiem jest stała. 
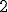
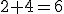
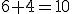
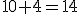
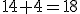
itd.
Zdefiniujmy porządniej to pojęcie.
Ciąg jest arytmetyczny, jeśli istnieje stała liczba
taka, że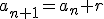 
Liczba
zwana jest różnicą ciągu.Są trzy przypadki jeśli chodzi o
1)
jest dodatnie - ciąg jest rosnący. Każdy następny wyraz jest większy (o stałą liczbę) od poprzednika.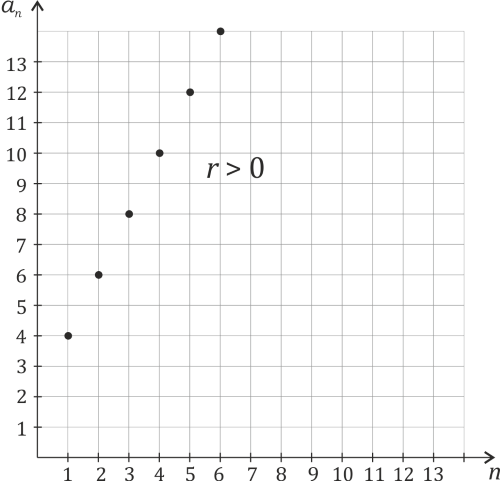
2)
jest ujemne - ciąg jest malejący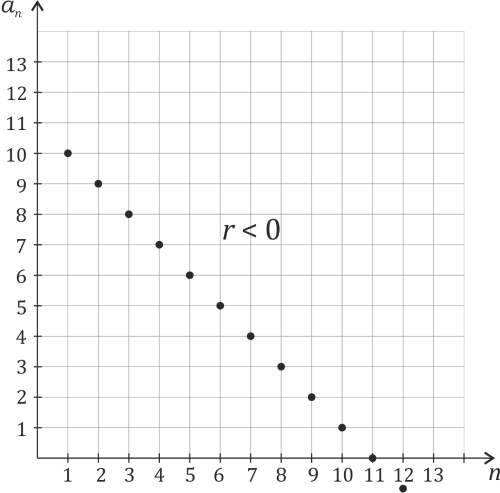
3)
równe zeru - ciąg stały.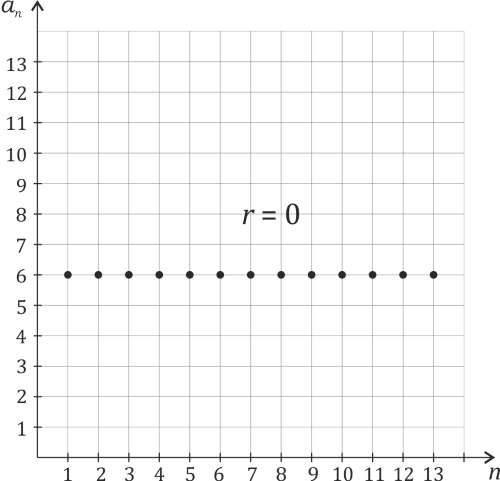
Nasza definicja należy do rekurencyjnych. Dobrze byłoby mieć wzór ogólny ciągu. Jest on następujący:
\cdot r)
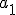- pierwszy wyraz
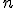- numer wyrazu ciągu - różnica ciąguDlaczego tak? Można zamiast dowodu przeprowadzić taką agitację. Wyraz drugi otrzymamy dodając do pierwszego
. Trzeci gdy do drugiego dodamy . To już dwa razy dodaliśmy . Następne dodajemy by otrzymać wyraz czwarty itd. Zwróćcie uwagę, że by otrzymać 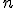-ty wyraz należy do 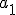dodać tyle razy, jaki jest numer tego wyrazu mniej 1. Mamy więc: r)
.Jak się już ma wzór ogólny ciągu arytmetycznego, nietrudno dowieść pewnej ważnej własności tego ciągu. Ze wspomnianego wzoru mamy:
, r=a_1+(n-2)r)
, r=a_1+nr)
.r+a_1+nr=2a_1+2(n-1)r=2a_n)
Stąd
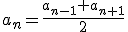
Słownie: dowolny (poza pierwszym i ewentualnym ostatnim) wyraz ciągu arytmetycznego jest średnią arytmetyczną wyrazów sąsiednich.
Suma
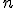początkowych wyrazów ciągu arytmetycznegoSpróbujmy uzyskać wzór na sumę
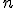początkowych wyrazów ciągu arytmetycznego. Sumę tę oznaczmy 
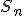. Przedstawmy ciąg arytmetyczny graficznie. Niech zarówno 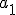jak i będą dodatnie. Taki ciąg przedstawiony na wykresie slupkowym będzie wyglądał jak na poniższym rysunku.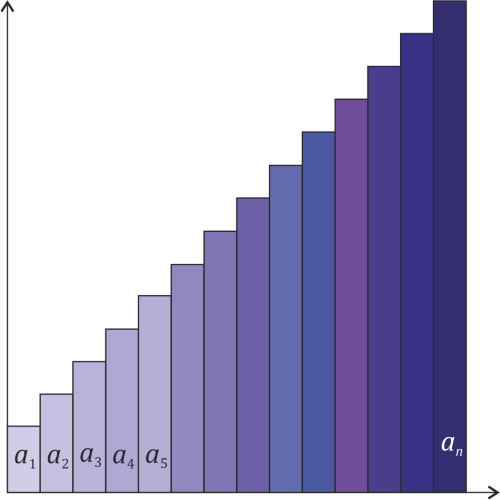
Suma
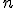wyrazów ciągu to suma długości 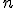słupków. Skopiujmy ten wykres, obróćmy go o 
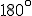i połączmy z pierwotnym wykresem jak na rysunku poniżej.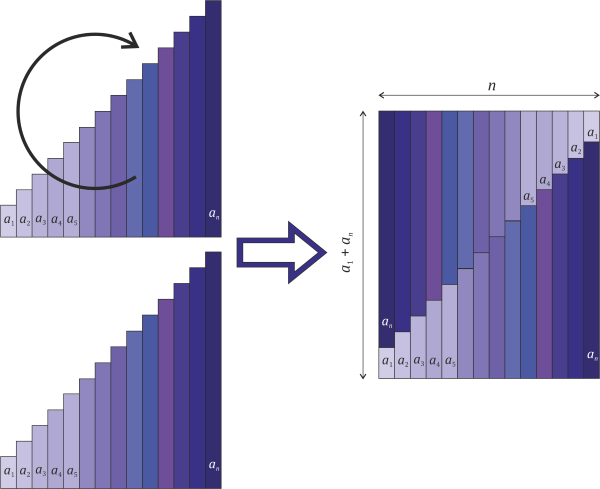
Otrzymujemy w ten sposób prostokąt o wymiarach
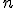i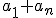 
. Suma długości słupków w tak zmodyfikowanym wykresie to dwie sumy, które chcemy obliczyć, a jednocześnie to "pole" tego prostokąta, czyli \cdot n)
Mamy więc
n)
.Wynika z tego, że
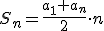
Wzór ten przypomina wzór na pole trapezu i, gdy przyjrzycie się przedostatniemu rysunkowi, zrozumiecie, ze to nie przypadek.
Dalsza część kursu dostępna
dla użytkowników 
premium
Subskrypcja premium miesięczna
Automatyczna comiesięczna płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT.
Płatność kartą. Autoodnawialność można w każdej chwili wyłączyć.
Dostęp premium na 3 miesiące
Jednorazowa płatność nadająca użytkownikowi dostęp do wszystkich materiałów edukacyjnych w portalu SOFIZMAT przez 3 miesiące.
Wszystkie metody płatności: szybki przelew, BLIK, karta, Google Pay.
Szybka i bezpieczna płatność za pomocą PayU. Wszystkie podane ceny zawierają podatek VAT.
- Tysiące kursów, zadań oraz quizów z matematyki i fizyki stworzonych przez ekspertów
- Podzielone tematycznie i ułożone tak, by zwiększyć efektywność uczenia się
- Pełny i wygodny dostęp z dowolnego urządzenia, komputera, tabletu lub komórki
- Najtańszy i najefektywniejszy sposób przygotowania się do matury
- Brak reklam i jakichkolwiek ukrytych kosztów
Chcesz otrzymać fakturę? Napisz na: .
Materiały zamieszczone w portalu SOFIZMAT podlegają ochronie prawnej na podstawie przepisów ustawy z dnia 4 lutego 1994 r. o prawie autorskim i prawach pokrewnych. Bez zgody właścicieli zabronione jest m.in. ich kopiowanie, przedruk oraz udostępnianie w całości, jak i w części.